La fusión nuclear. La energía de las estrellas

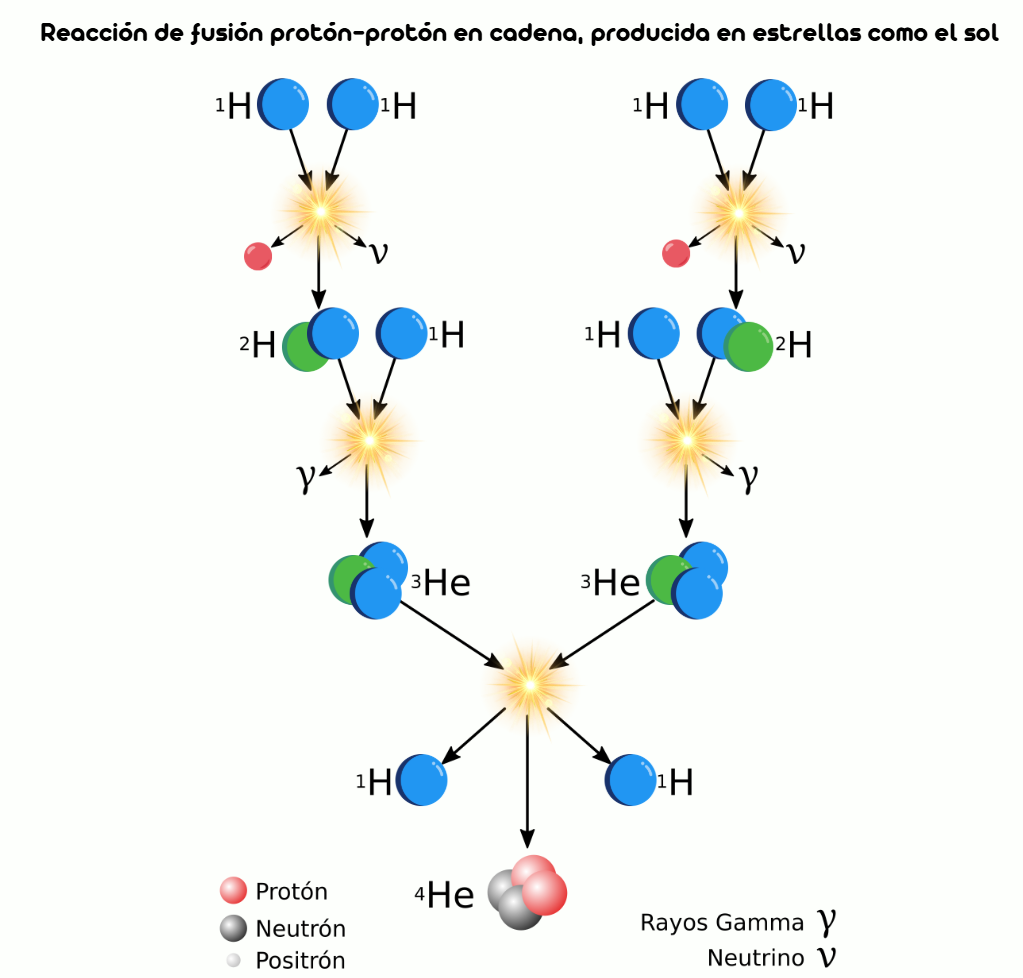
Cuando miramos al Sol, estamos viendo un reactor de fusión natural funcionando desde hace 4.600 millones de años, donde el ciclo protón-protón es la principal fuente de energía. En su interior, bajo condiciones extremas de temperatura y presión, se producen reacciones de fusión nuclear que convierten hidrógeno en helio, liberando enormes cantidades de energía.

Su luz y calor sostienen la vida en la Tierra, y conforma lo que se conoce como región de habitabilidad. La región de habitabilidad (a menudo llamada zona habitable) en un sistema estelar es la franja de distancias alrededor de una estrella donde las condiciones permiten, en principio, la existencia de agua líquida en la superficie de un planeta rocoso. El agua líquida se considera clave porque es un solvente universal para procesos bioquímicos conocidos y esencial para la vida tal como la entendemos en la Tierra.
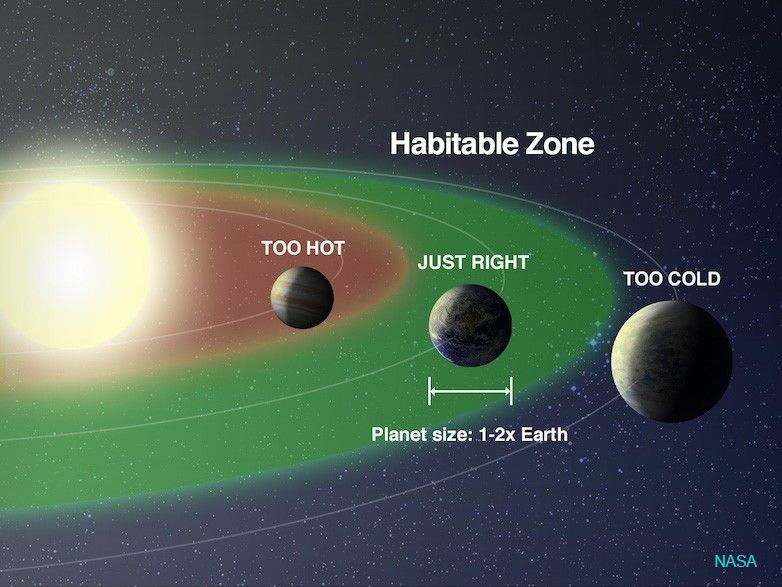
Esta región depende de la luminosidad de la estrella, de su espectro, de las atmósferas y albedo de los planetas en órbita, y de periodos de gran estabilidad que permitan la evolución biológica.
En resumen, no podemos imaginar la vida en el universo tal y como la conocemos sin la presencia de estos astros que radian cantidades colosales de energía.
¿Cómo producen esa energía?
La energía de las estrellas proviene de las reacciones de fusión que tienen lugar en su interior. En el núcleo del Sol reinan condiciones extremas: temperaturas de 15 millones de grados y presiones aplastantes. Allí, los núcleos de hidrógeno (protones) se mueven tan rápido que pueden superar su repulsión eléctrica y fusionarse para formar helio.
¿Qué es la fusión?
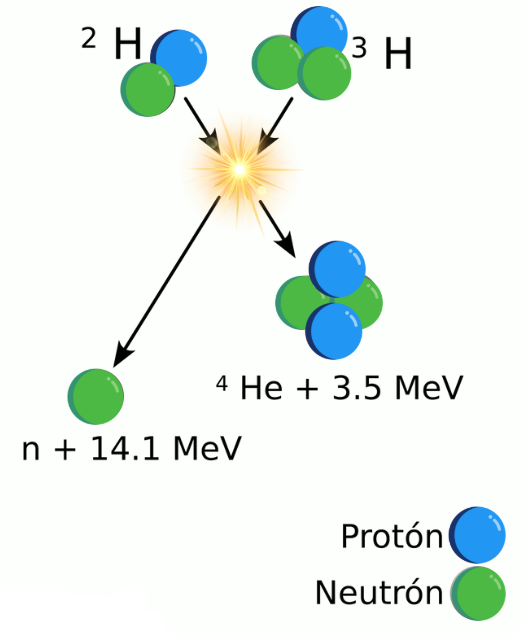
La fusión es un proceso que consiste en la unión de dos núcleos ligeros para formar, al menos, un núcleo más pesado y estable. Para que la reacción de fusión libere energía, el combustible ha de estar formado por núcleos ligeros, de lo contrario requerirá energía adicional. Una de las reacciones de fusión más célebres, por su importancia en los reactores actuales, es la fusión de deuterio y tritio, donde un núcleo de deuterio se fusiona con un núcleo de tritio dando como resultado un núcleo de helio-4, un neutrón libre y una energía de unos 17.6 MeV (14.1 + 3.5).
El Sol lleva en la secuencia principal (fusionando hidrógeno en helio) unos 4.600 millones de años y se espera que continúe así otros ~5.000 millones de años, hasta agotar el hidrógeno de su núcleo. Su estabilidad se debe al equilibrio hidrostático entre la presión de radiación generada por la fusión (que tiende a expandir la estrella) y la gravedad (que tiende a contraerla).
Ahora bien, ¿de dónde proviene esa energía de las reacciones?
Al igual que en las reacciones de fisión, la energía de una reacción de fusión nuclear proviene directamente del déficit de masa que aparece al comparar la masa de los núcleos iniciales con la masa del núcleo final y las partículas resultantes.
Según la ecuación de Einstein, la masa y la energía son equivalentes.
Cuando dos núcleos ligeros se fusionan:
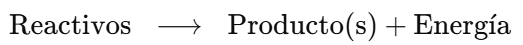
se observa que la masa de los productos es ligeramente menor que la masa de los reactivos.
Esa diferencia de masa (Δm) se transforma en energía liberada:
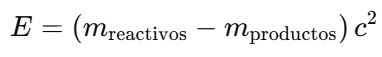
Cada núcleo tiene una energía de enlace (la energía que mantiene unidos a protones y neutrones). Cuando se fusionan núcleos ligeros (H, D, T, He, etc.), los productos tienen una energía de enlace por nucleón mayor → están más “fuertemente ligados”. Al ganar estabilidad, “sobran” unos MeV por nucleón, que se liberan en forma de energía cinética de las partículas y radiación.
¿Es posible simular estas condiciones en la Tierra?
No es posible reproducir simultáneamente las tres magnitudes (temperatura, densidad y presión) del núcleo solar. Es decir, en el centro del Sol, la temperatura es de unos 15 millones de grados, la densidad ronda las 150 g/cm3 y la presión es del orden de 1016 Pa.
Estas condiciones son posibles debido a que el Sol confina al plasma mediante su potente campo gravitatorio, ya que su enorme masa (≈ 2×1030 kg) genera una gravedad que produce presiones colosales en su núcleo. Esta presión comprime el plasma a densidades muy altas, manteniendo a los núcleos lo suficientemente cerca y durante el tiempo suficiente para que ocurra la fusión, aunque la temperatura sea relativamente "modesta". Como era de esperar, estas condiciones de presión quedan fuera de nuestro alcance en la Tierra. La solución para lograr la fusión pasa por las siguientes alternativas:
- Confinamiento inercial:
- Comprimen una cápsula de combustible (generalmente deuterio-tritio) a densidades enormes (cercanas o superiores a la del Sol, hasta 1000 g/cm³).
- El plasma dura nanosegundos, pero alcanza las condiciones para producir ignición y ganancia neta de energía.
- Confinamiento magnético:
- Alcanzan temperaturas mucho más altas que en el Sol, del orden de 100–150 millones de kelvin.
- La densidad es muy baja (similar a un buen vacío, del orden de 1020 partículas/m3 ) nada que ver con el centro solar.
- Se confina el plasma con campos magnéticos durante segundos.
- Se usan reacciones más rápidas que la cadena p-p, típicamente deuterio-tritio (D-T), con secciones eficaces mucho mayores.
Concluyendo, no podemos recrear al 100% las condiciones del Sol, o cualquier otra estrella en la Tierra (al menos por el momento), dado que no podemos alcanzar esas densidades y presiones de manera estable y sostenida. Lo que si es posible es producir reacciones de fusión bajo condiciones distintas: temperaturas más altas y densidades más bajas, o al revés, densidades muy altas y tiempos muy cortos.
Criterio de Lawson
Previamente se han planteado los posibles ‘atajos’ que permiten la fusión en la Tierra con nuestra tecnología actual, pero ¿cuáles son las condiciones mínimas que deben cumplirse?
Es ahí donde entra en juego al denominado criterio de Lawson, que establece las condiciones mínimas que un plasma debe cumplir para que una reacción de fusión sea autosostenida o produzca ganancia neta de energía.
Se formula con el triple producto: n T τE
donde:
- n = densidad de partículas del plasma [m-3]
- T = temperatura [keV]
- τE= tiempo de confinamiento de energía (cuánto tiempo se mantiene la energía en el plasma antes de perderse).
Por el momento, la reacción más prometedora, por ser la más 'asequible' (es la que presenta la mayor sección eficaz entre las reacciones de fusión práctica) es el deuterio-tritio (D-T). El criterio de Lawson establece que para la ignición en la reacción D–T se requiere nTτE ≳ 1021
Por poner en contexto la complejidad de recurrir a otro tipo de reacciones que no sean la D-T:
- D–D: requiere un triple producto unas 100 veces mayor que D–T, lo que lo hace mucho más difícil.
- p–B¹¹ (protones + boro-11): requiere unas 10 000 veces más, pero produce mucha menos radiación de neutrones.
¿Cómo se adapta cada tipo de confinamiento al criterio de Lawson?
- Confinamiento gravitatorio (estrellas)
- n: muy alto (≈ 1032 m-3)
- T: relativamente bajo (≈ 1.3 keV ≈ 15 MK).
- τE: enorme, del orden de millones de años.
Cumple el criterio gracias a densidad y tiempo de confinamiento enormes, aunque la temperatura sea baja. La fusión que predomina es la cadena protón-protón (p-p), muy lenta pero suficiente para mantener al Sol estable.
- Confinamiento magnético
- n: bajo, vacío denso ≈ 1019-21 m-3
- T: muy alto, ≈ 10–20 keV (100–200 MK).
- τE: moderado, 1–10 s en los reactores experimentales actuales.
Cumple el criterio con temperaturas muy altas y un tiempo de confinamiento magnético suficientemente largo.
- Confinamiento inercial
- n: altísimo, comparable o mayor que el núcleo del Sol (≈ 1031-33 m-3).
- T: alto, ≈ 10–20 keV.
- τE: muy corto, solo nanosegundos (10-9 s).
Cumple el criterio gracias a la densidad extrema, que compensa el tiempo minúsculo de confinamiento. De hecho, se alcanza la ignición cuando la energía liberada supera a las pérdidas en ese brevísimo intervalo.
| Confinamiento | Densidad | Temperatura | Tiempo | Estrategia |
|---|---|---|---|---|
| Gravitatorio (Sol) | Muy alta | Relativamente baja | Muy largo | Densidad + tiempo |
| Magnético (Tokamak) | Baja | Muy alta | Largo (segundos) | Temperatura + tiempo |
| Inercial (Láseres) | Muy alta | Alta | Muy corto | Densidad extrema |





